Flow Simulation: Computational Domain Editing Part 2 – Periodicity

In Part 1 of this blog series, I covered the SOLIDWORKS Flow Simulation computational domain symmetry condition setting to reduce the size of the computational fluid dynamics (CFD) problem to be solved. The result is a decreased solution time and required computer memory. This blog will show how another computational domain condition, periodicity, can be used in those situations where you have a pattern of identical components in the flow field.

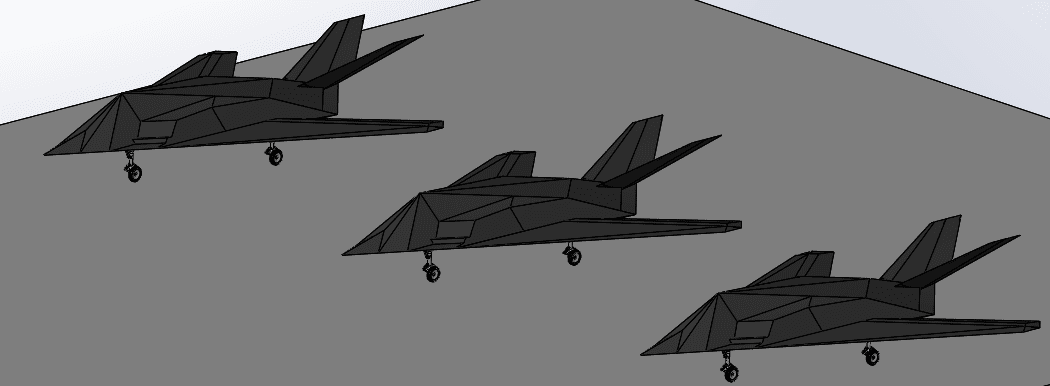
I’ll continue to use the Lockheed F-117 Nighthawk stealth fighter for this blog, simulating the airflow over a group of aircraft parked on the tarmac.

https://www.lockheedmartin.com/en-us/news/features/history/f-117.html

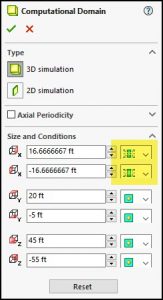
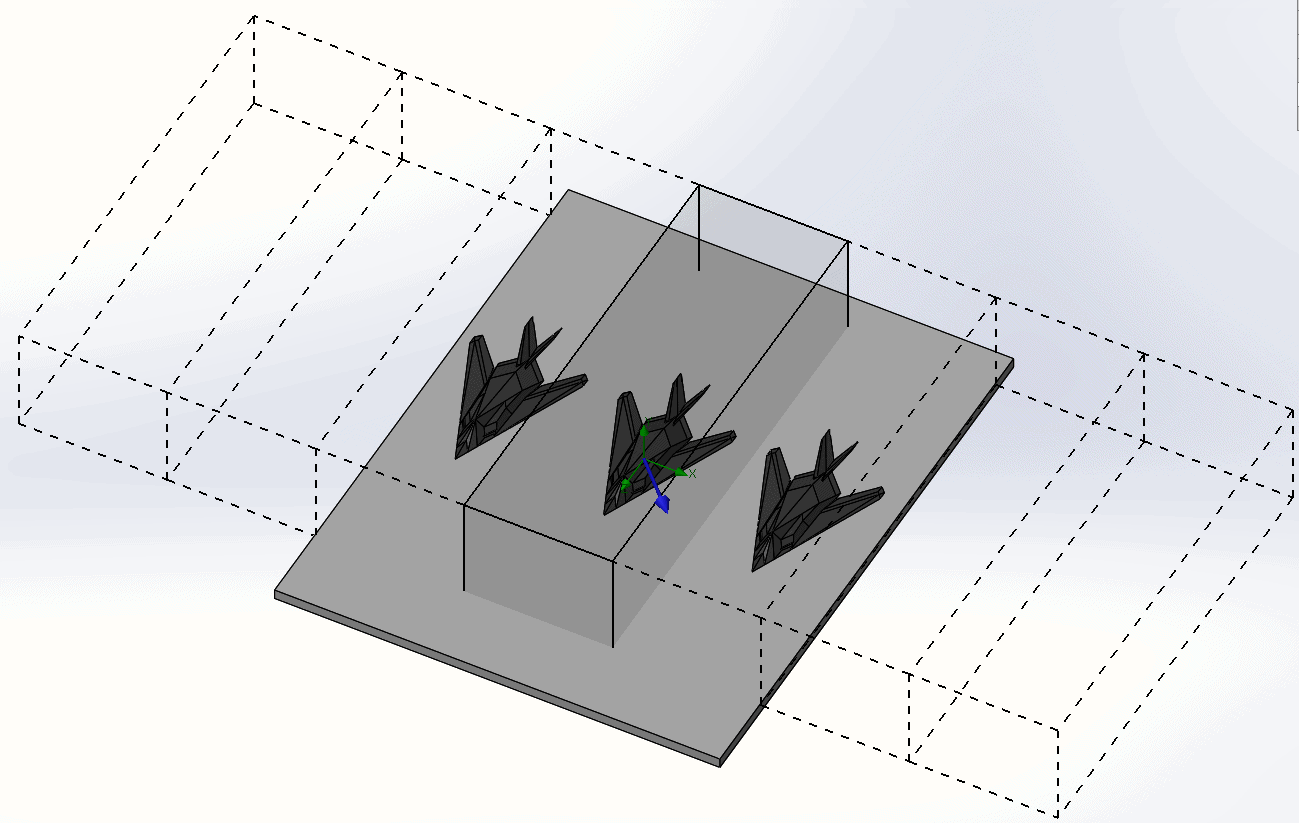
With the periodicity condition turned on we can resize the computational domain to include only one airplane and see the effect on the flow field if multiple planes were actually present. Notice that the periodicity condition has been activated, as shown in the highlighted box next to the X-direction domain size setting. The other directions maintain the default condition.

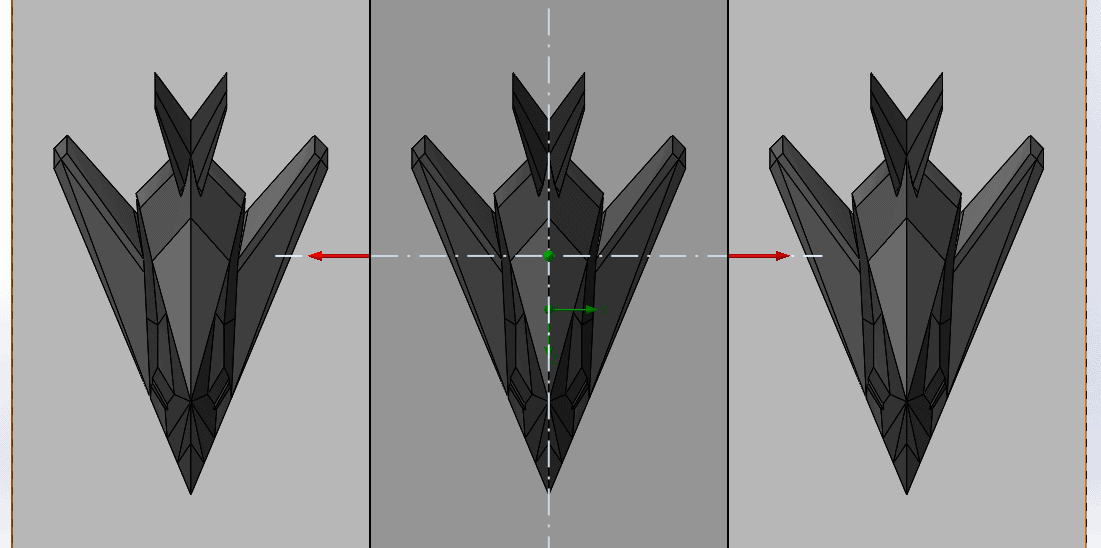
The computational domain boundary is shown below. Solid lines surrounding the middle aircraft indicate that only it will be captured in the solution, while the dashed line boundaries show that the effect of the others will be included due to the periodicity setting. This is an external flow analysis and I’ve added ambient conditions to generate an airflow of approximately 20 MPH in the X- and Z- directions with the resultant vector indicated by the blue arrow.

After completing the solution, a cut plot generated near the center of the aircraft fuselage shows the velocity field with streamlines. The highest velocity, colored red, occurs where the air moves around the tail section. Stagnant airflow, colored blue, shows up near the tail on the downwind side of the fuselage.

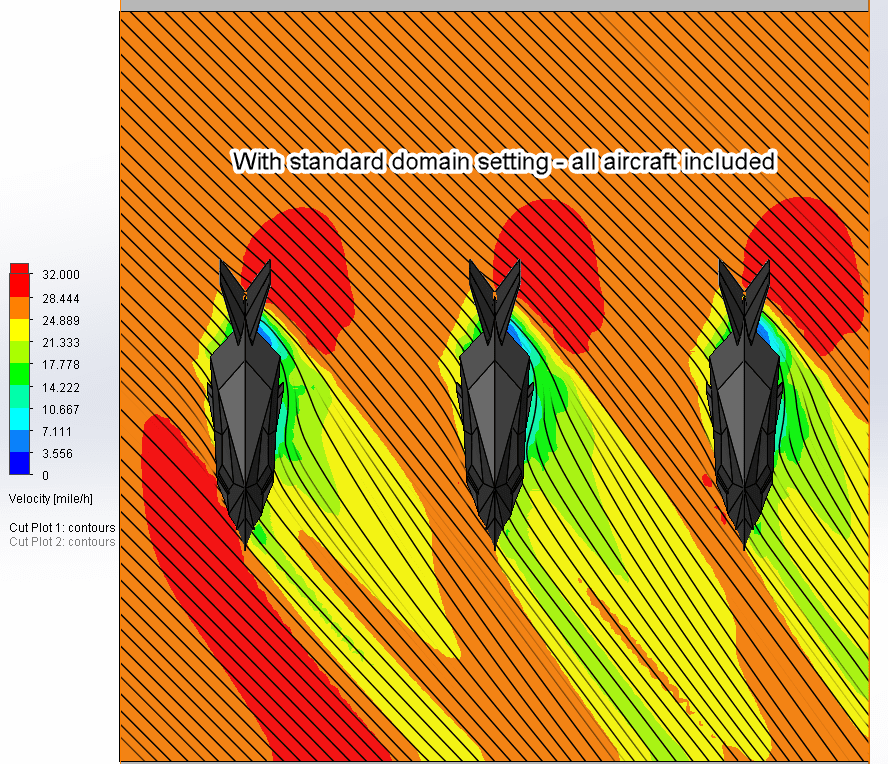
A solution with a standard domain that includes all three aircraft was also performed for comparison. A similar airflow pattern is observed around the two on the right side. The upstream plane has a different pattern, as expected. This is one limitation of using this condition. It produces results that exclude the real effect of the first upstream item – it treats the problem like there is an infinite number of aircraft in line. In reality, the flow accelerates as it passes by the first aircraft, as shown in the solution without periodicity, but this isn’t captured in the solution using periodicity.

What’s the advantage of using the periodicity domain condition? Time and resource savings! Just like the symmetry condition discussed in Part 1, this condition significantly reduces the size of the problem. Whereas the reduction with symmetry is proportional to the number of symmetry planes, the reduction for periodicity depends on the number of items captured virtually. In our case, we reduced the size of the problem by a factor of three.

Another practical application of this feature is a cooling calculation for a stacked group of similar devices as you might find in a rack of electronic components. In such a scenario there are likely to be many components in each group with small passageways in which the air can flow, which might make a full solution impractical or impossible without the use of the periodicity condition. Maybe you can think of other ways to apply this to your product design efforts.

Thanks for reading! I hope you are able to advantageously use the information I’ve presented to more efficiently analyze and develop your products.

Kurt Kurtin
Technical Manager, Simulation Products
Computer Aided Technology, LLC