SOLIDWORKS: Magic of SOLIDWORKS Equation Driven Curves
Magic of SOLIDWORKS Equation Driven Curves
Most SOLIDWORKS users are comfortable creating models with the familiar sketch commands (lines, rectangles, splines, arcs, etc.); however, there are occasions when a design is dependent on mathematical functions or equations to describe its geometry/topology. Examples of this might be the curvature of a lens, the design of a custom spring, wind-foil, or perhaps a roller-coaster path. To create these special kinds of curves, the best approach would be to utilize the Equation Driven Curves command. This should not be confused with the Equations table where Global Variables are dealt with.
The first thing to keep in mind using this command is that it actually generates a spline, and so certain limitations will apply which I’ll discuss a little later. Also, because SOLIDWORKS evaluates functions and equations numerically, the command will not work for numbers or ranges that produce undefined outputs (e.g. 1/X where X = 0).
Equation Driven Curves can be found in sketch entities under “Splines”:
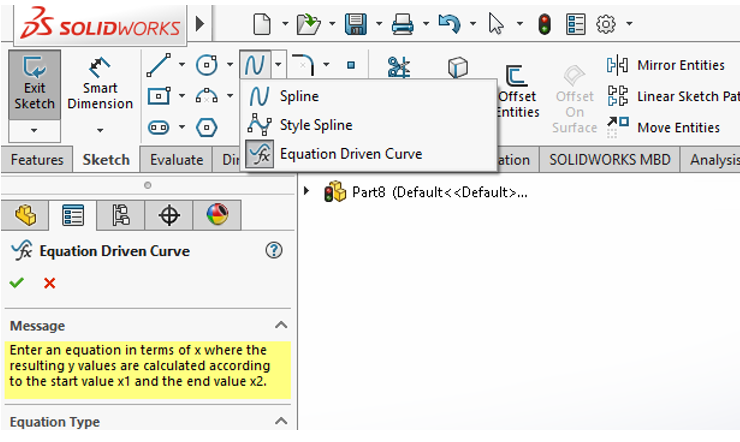
The command can be applied in both 2-D and 3-D space. To access 3-D curves, start a 3-D sketch and then choose Equation Driven Curve – otherwise it defaults to the 2-D setting in regular sketch mode.
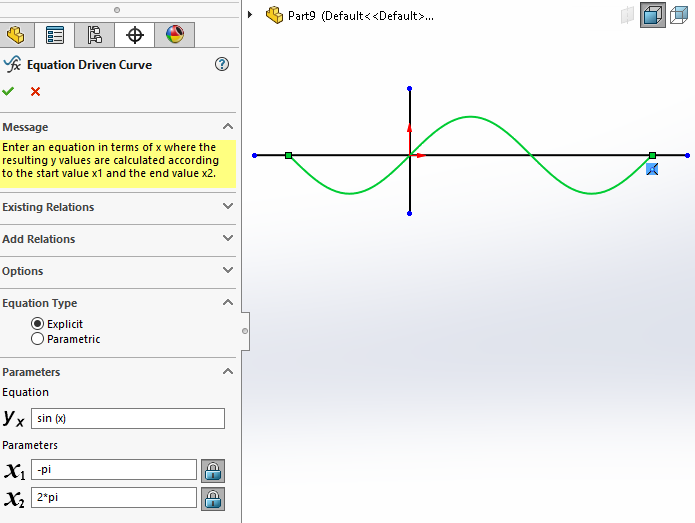
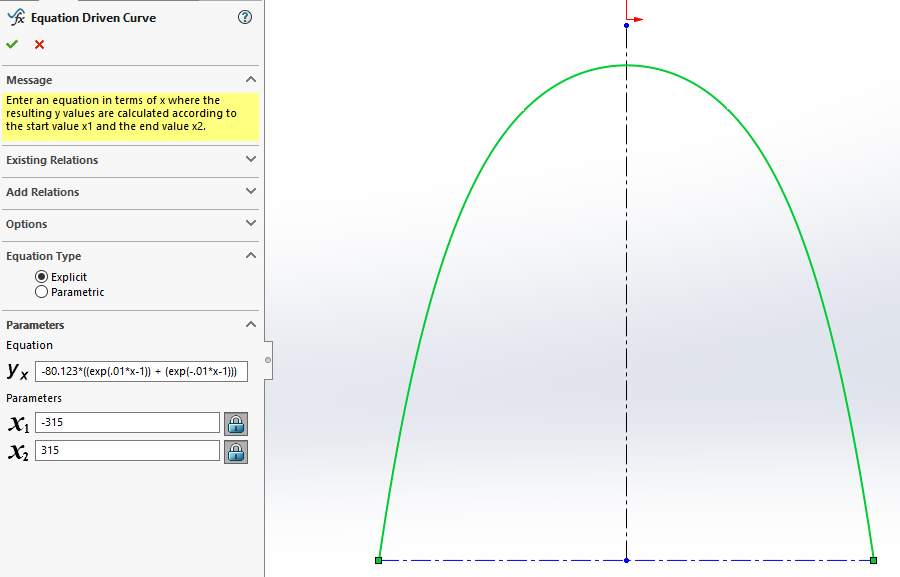
In this example of a sine-curve, leaving the Equation Type on “Explicit,” we can see the yx field takes the equation in terms of “x” while x1 and x2 establish the range of values evaluated for “x” in the equation. The curve is generated and referenced from the origin (0,0). Notice that the x-axis is interpreted as length instead of radians or degrees in this case.
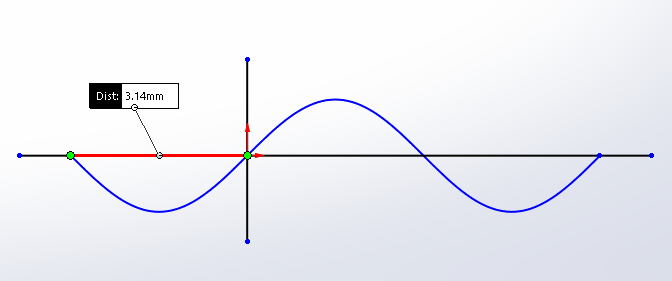
Once an equation curve is generated, it can be positioned and integrated into a design as desired.

The following is a list of available mathematical functions in SOLIDWORKS Equation Driven Curves:

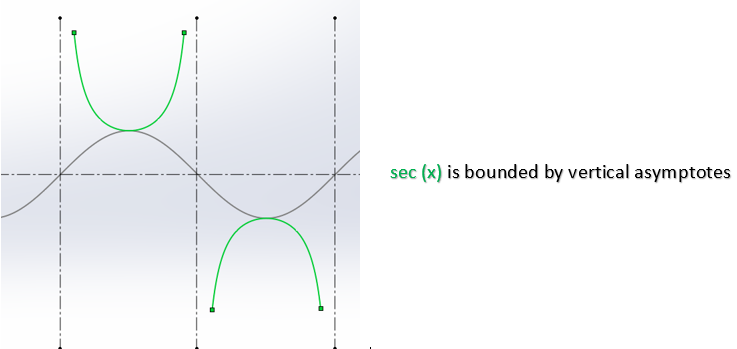
Watch out when defining the range of inputs for “x” as some functions are undefined in certain regions. For example, sec(x) is asymptotic and only works over specific ranges such as -1.5 < x < 1.5 or 1.6 < x < 4.6 etc.
As with any numerical input, order-of-operations applies. This means proper placement of parentheses is crucial in getting correct results. For example, 1/6+4 ≠ 1/(6+4). Also keep in mind, negative exponents must be enclosed in parentheses. If the syntax happens to be wrong, the equation will highlight as a red color.
Imaginary and complex numbers are not included in this command.
There are also no commands for hyperbolic trig functions (e.g. cosh(x), sinh(x), etc.); however, these can be re-written in terms of ex such as: cosh(x) = (ex + e-x)/2. The St. Louis Gateway Arch was designed based on the Catenary function using cosh(x).

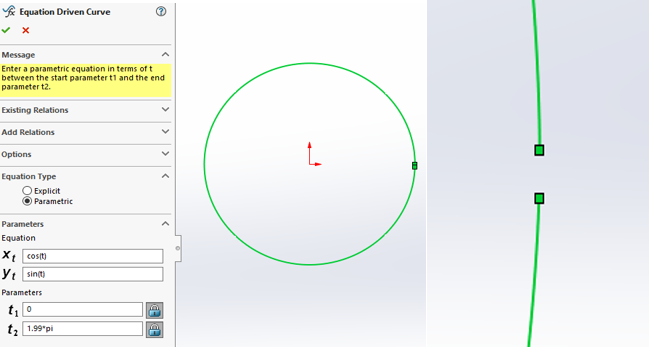
For 2D sketches, SOLIDWORKS allows the input of parametric equation types. However, because t1 and t2 represent the start and end points of a spline, they can never coexist at the same location. Please keep this in mind when working with parametric equation types.
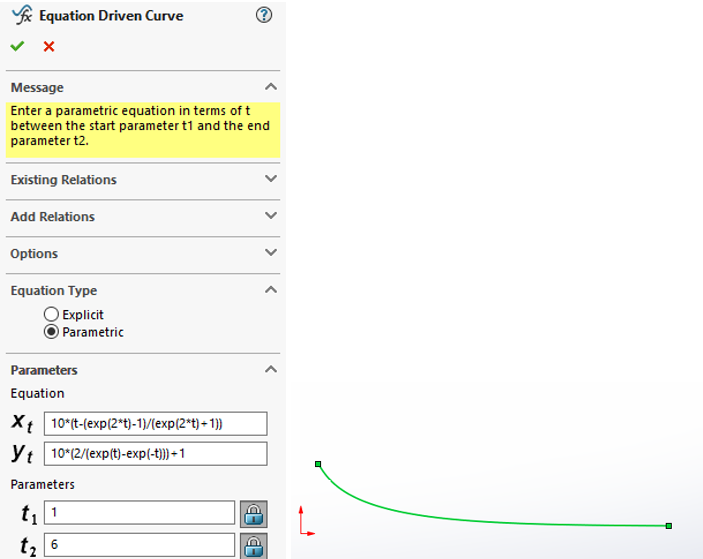
Parametric curves can be used to create various solids. For example, starting with a baseline equation for a trumpet bell, the curve can be revolved into a solid with parameters easily modified:

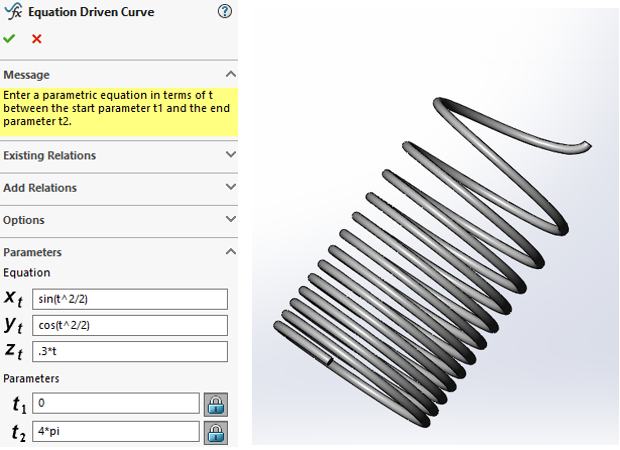
3D equation driven curves are also possible in SOLIDWORKS with the addition of a “Z” coordinate. Take for example, customized spring design:
Or the creation of special surfaces without using the unpredictable freeform surfacing tool:
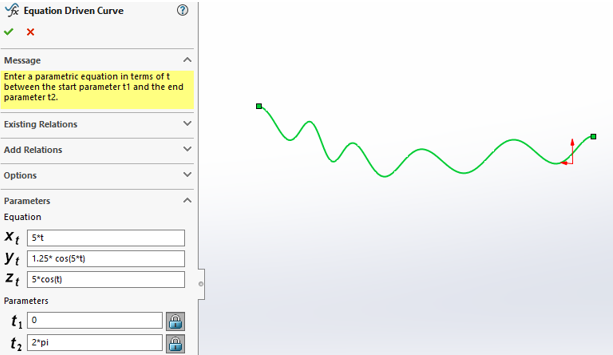
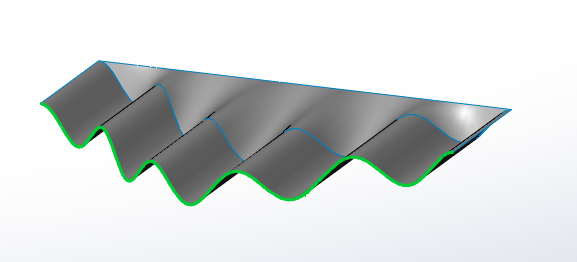
The applications for mathematical equations in design are endless. Whether you are trying to create the best flow contour of a wind tunnel, curve on a propeller blade, or sailboat hull shape, SOLIDWORKS Equation Driven Curve is the best, most powerful and efficient way to approach it. I hope you found this article helpful and as always, be sure to contact Computer Aided Technology technical support for any SOLIDWORKS questions you may have.
James Carlin
Application Engineer
Computer Aided Technology

 Blog
Blog